Aangrenzende en verticale hoeken 1 niveau. Injectie

24.09.2019

HOOFDSTUK I.

BASISCONCEPTEN.

§elf. AANgrenzende EN VERTICALE HOEKEN.

1. Aangrenzende hoeken.

Als we de zijkant van een hoek voorbij het hoekpunt voortzetten, krijgen we twee hoeken (Fig. 72): / een zon en / SVD, waarbij één zijde BC gemeenschappelijk is, en de andere twee AB en BD een rechte lijn vormen.

Twee hoeken die één zijde gemeen hebben en de andere twee een rechte lijn vormen, worden aangrenzende hoeken genoemd.

Aangrenzende hoeken kunnen ook op deze manier worden verkregen: als we een straal tekenen vanaf een punt op een rechte lijn (niet liggend op een bepaalde rechte lijn), dan krijgen we aangrenzende hoeken.
Bijvoorbeeld, / ADF en / FDВ - aangrenzende hoeken (Fig. 73).

Aangrenzende hoeken kunnen verschillende posities hebben (Fig. 74).

Aangrenzende hoeken vormen samen een rechte hoek, dus ummah van twee aangrenzende hoeken is gelijk aan 2D.

Daarom kan een rechte hoek worden gedefinieerd als een hoek die gelijk is aan de aangrenzende hoek.

Als we de waarde van een van de aangrenzende hoeken kennen, kunnen we de waarde van de andere aangrenzende hoek vinden.

Als een van de aangrenzende hoeken bijvoorbeeld 3/5 . is D, dan is de tweede hoek gelijk aan:

2D- 3 / 5 D= l 2 / 5 D.

2. Verticale hoeken.

Als we de zijden van een hoek buiten zijn toppunt verlengen, krijgen we verticale hoeken. In tekening 75 zijn de hoeken EOF en AOC verticaal; hoeken AOE en COF zijn ook verticaal.

Twee hoeken worden verticaal genoemd als de zijden van de ene hoek verlengingen zijn van de zijden van de andere hoek.

laten zijn / 1 = 7 / 8 D(Afb. 76). Ernaast / 2 is gelijk aan 2 D- 7 / 8 D, d.w.z. 1 1/8 D.

Op dezelfde manier kun je berekenen wat gelijk is aan / 3 en / 4.
/ 3 = 2D - 1 1 / 8 D = 7 / 8 D; / 4 = 2D - 7 / 8 D = 1 1 / 8 D(Afb. 77).

We zien dat / 1 = / 3 en / 2 = / 4.

Je kunt meerdere van dezelfde problemen oplossen, en elke keer krijg je hetzelfde resultaat: de verticale hoeken zijn gelijk aan elkaar.

Om er echter voor te zorgen dat de verticale hoeken altijd gelijk zijn aan elkaar, is het niet voldoende om individuele numerieke voorbeelden te beschouwen, omdat conclusies die uit bepaalde voorbeelden worden getrokken soms onjuist kunnen zijn.

Het is noodzakelijk om de geldigheid van de eigenschap van verticale hoeken te verifiëren door te redeneren, door bewijs.

Het bewijs kan als volgt worden uitgevoerd (afb. 78):

/ een +/ C = 2D;
/ b +/ C = 2D;

(aangezien de som van aangrenzende hoeken 2 . is D).

/ een +/ C = / b +/ C

(aangezien de linkerkant van deze gelijkheid gelijk is aan 2 D, en de rechterkant is ook gelijk aan 2 D).

Deze gelijkheid omvat dezelfde hoek van.

Als we gelijkelijk van gelijke waarden aftrekken, blijft het gelijk. Het resultaat zal zijn: / een = / B d.w.z. de verticale hoeken zijn gelijk aan elkaar.

Bij het beschouwen van de kwestie van verticale hoeken, hebben we eerst uitgelegd welke hoeken verticaal worden genoemd, d.w.z. we gaven definitie verticale hoeken.

Toen hebben we een oordeel (uitspraak) gedaan over de gelijkheid van verticale hoeken en waren we overtuigd van de geldigheid van dit oordeel door bewijs. Dergelijke oordelen, waarvan de geldigheid moet worden bewezen, worden stellingen. In deze sectie hebben we dus de definitie van verticale hoeken gegeven en ook een stelling over hun eigenschap verklaard en bewezen.

In de toekomst zullen we bij het bestuderen van meetkunde voortdurend te maken krijgen met definities en bewijzen van stellingen.

3. De som van hoeken die een gemeenschappelijk hoekpunt hebben.

Op de tekening 79 / 1, / 2, / 3 en / 4 bevinden zich aan dezelfde kant van een rechte lijn en hebben een gemeenschappelijk hoekpunt op deze rechte lijn. Samengevat vormen deze hoeken een rechte hoek, d.w.z.
/ 1+ / 2+/ 3+ / 4 = 2D.

Op de tekening 80 / 1, / 2, / 3, / 4 en / 5 hebben een gemeenschappelijke top. Samengevat vormen deze hoeken een volledige hoek, d.w.z. / 1 + / 2 + / 3 + / 4 + / 5 = 4D.

Opdrachten.

1. Een van de aangrenzende hoeken is 0,72 D. Bereken de hoek gevormd door de bissectrices van deze aangrenzende hoeken.

2. Bewijs dat de bissectrices van twee aangrenzende hoeken een rechte hoek vormen.

3. Bewijs dat als twee hoeken gelijk zijn, hun aangrenzende hoeken ook gelijk zijn.

4. Hoeveel paar aangrenzende hoeken zijn er in tekening 81?

5. Kan een paar aangrenzende hoeken bestaan uit twee scherpe hoeken? uit twee stompe hoeken? vanuit rechte en stompe hoeken? vanuit een rechte en scherpe hoek?

6. Als een van de aangrenzende hoeken juist is, wat kan er dan gezegd worden over de waarde van de aangrenzende hoek?

7. Als er op het snijpunt van twee rechte lijnen één rechte hoek is, wat kan er dan gezegd worden over de grootte van de overige drie hoeken?

In deze les zullen we het concept van aangrenzende hoeken overwegen en begrijpen. Overweeg de stelling die hen aangaat. Laten we het concept van "verticale hoeken" introduceren. Overweeg de ondersteunende feiten met betrekking tot deze hoeken. Vervolgens formuleren en bewijzen we twee uitvloeisels over de hoek tussen de bissectrices van verticale hoeken. Aan het einde van de les zullen we verschillende taken bespreken die aan dit onderwerp zijn gewijd.

Laten we onze les beginnen met het concept van "aangrenzende hoeken". Figuur 1 toont de ontwikkelde hoek ∠AOC en de straal OB, die deze hoek in 2 hoeken verdeelt.

Rijst. 1. Hoek (AOC)

Beschouw de hoeken ∠AOB en ∠BOC. Het is vrij duidelijk dat ze een gemeenschappelijke kant VO hebben, terwijl de kanten AO en OS tegenovergesteld zijn. Stralen OA en OS vullen elkaar aan, wat betekent dat ze op dezelfde rechte lijn liggen. De hoeken ∠AOB en ∠BOC zijn aangrenzend.

Definitie: Als twee hoeken een gemeenschappelijke zijde hebben en de andere twee zijden complementaire stralen zijn, dan worden deze hoeken genoemd verwant.

Stelling 1: De som van aangrenzende hoeken is 180 o.

Rijst. 2. Tekenen voor Stelling 1

∠MOL + ∠LON = 180o. Deze bewering is waar omdat de straal OL de gestrekte hoek ∠MON in twee aangrenzende hoeken verdeelt. Dat wil zeggen, we kennen de graadmaten van geen van de aangrenzende hoeken, maar we kennen alleen hun som - 180 o.

Beschouw het snijpunt van twee lijnen. De figuur toont het snijpunt van twee lijnen in punt O.

Rijst. 3. Verticale hoeken BOA en ∠COD

Definitie: Als de zijden van een hoek een voortzetting zijn van de tweede hoek, dan worden zulke hoeken verticaal genoemd. Daarom toont de figuur twee paar verticale hoeken: ∠AOB en ∠COD, evenals ∠AOD en ∠BOC.

Stelling 2: Verticale hoeken zijn gelijk.

Laten we figuur 3 gebruiken. Laten we eens kijken naar de ontwikkelde hoek ∠AOC. ∠AOB \u003d ∠AOC - ∠BOC \u003d 180 o - β. Beschouw de ontwikkelde hoek ∠BOD. ∠COD = ∠BOD - ∠BOC = 180 o - β.

Uit deze overwegingen concluderen we dat ∠AOB = ∠COD = α. Evenzo geldt ∠AOD = ∠BOC = β.

Gevolg 1: De hoek tussen de bissectrices van aangrenzende hoeken is 90°.

Rijst. 4. Tekenen voor gevolg 1

Aangezien OL de bissectrice is van de hoek ∠BOA, dan is de hoek ∠LOB = , vergelijkbaar met ∠BOK = . ∠LOK = ∠LOB + ∠BOK = + = . De som van de hoeken α + β is gelijk aan 180 o, aangezien deze hoeken aangrenzend zijn.

Gevolg 2: De hoek tussen de bissectrices van de verticale hoeken is 180°.

Rijst. 5. Tekenen voor gevolg 2

KO is de bissectrice van ∠AOB, LO is de bissectrice van ∠COD. Het is duidelijk dat ∠KOL = ∠KOB + ∠BOC + ∠COL = o . De som van de hoeken α + β is gelijk aan 180 o, aangezien deze hoeken aangrenzend zijn.

Laten we eens kijken naar enkele taken:

Zoek de hoek naast ∠AOC als ∠AOC = 111 o.

Laten we een tekening maken voor de taak:

Rijst. 6. Tekenen bijvoorbeeld 1

Aangezien ∠AOC = β en ∠COD = α aangrenzende hoeken zijn, dan is α + β = 180 o. Dat wil zeggen, 111 o + β \u003d 180 o.

Vandaar, β = 69 o.

Dit type probleem maakt gebruik van de stelling van de aangrenzende hoeksom.

Een van de aangrenzende hoeken is een rechte hoek, welke (acuut, stomp of rechts) is de andere hoek?

Als een van de hoeken goed is en de som van de twee hoeken is 180°, dan is de andere hoek ook goed. Deze taak test kennis over de som van aangrenzende hoeken.

Klopt het dat als aangrenzende hoeken gelijk zijn, ze ook rechte hoeken zijn?

Laten we een vergelijking maken: α + β = 180 o, maar aangezien α = β, dan β + β = 180 o, wat betekent β = 90 o.

Antwoord: Ja, de stelling is waar.

Gegeven twee gelijke hoeken. Klopt het dat de aangrenzende hoeken ook gelijk zijn?

Rijst. 7. Tekenen bijvoorbeeld 4

Als twee hoeken gelijk zijn aan α, dan zijn hun overeenkomstige aangrenzende hoeken 180 o - . Dat wil zeggen, ze zullen aan elkaar gelijk zijn.

Antwoord: De stelling is waar.

Alexandrov AD, Werner A.L., Ryzhik V.I. enz. Geometrie 7. - M.: Verlichting.
Atanasyan LS, Butuzov VF, Kadomtsev SB et al. Geometrie 7. 5e druk. - M.: Verlichting.
\Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometrie 7 / V.F. Butuzova, SB Kadomtsev, V.V. Prasolov, onder redactie van V.A. Sadovnichy. - M.: Onderwijs, 2010.

Meting van segmenten ().
Algemene les over meetkunde in het 7e leerjaar ().
Rechte lijn, segment ().

Nr. 13, 14. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometrie 7 / V.F. Butuzova, SB Kadomtsev, V.V. Prasolov, onder redactie van V.A. Sadovnichy. - M.: Onderwijs, 2010.
Vind twee aangrenzende hoeken als een van hen 4 keer de andere is.
Een hoek gegeven. Bouw er aangrenzende en verticale hoeken voor. Hoeveel van dergelijke hoeken kunnen worden gebouwd?
* In welk geval worden meer paren verticale hoeken verkregen: wanneer drie lijnen elkaar snijden op één punt of op drie punten?

Geometrie is een zeer veelzijdige wetenschap. Het ontwikkelt logica, verbeeldingskracht en intelligentie. Natuurlijk, vanwege de complexiteit en het enorme aantal stellingen en axioma's, vinden schoolkinderen het niet altijd leuk. Bovendien is het nodig om hun conclusies voortdurend te bewijzen aan de hand van algemeen aanvaarde normen en regels.

Aangrenzende en verticale hoeken zijn een integraal onderdeel van de geometrie. Zeker, veel schoolkinderen zijn dol op ze omdat hun eigenschappen duidelijk en gemakkelijk te bewijzen zijn.

Vorming van hoeken

Elke hoek wordt gevormd door het snijpunt van twee lijnen of door twee stralen vanuit één punt te trekken. Ze kunnen één letter of drie worden genoemd, die achtereenvolgens de bouwpunten van de hoek aanduiden.

Hoeken worden gemeten in graden en kunnen (afhankelijk van hun waarde) anders worden genoemd. Er is dus een rechte hoek, scherp, stomp en ingezet. Elk van de namen komt overeen met een bepaalde graadmaat of het interval ervan.

Een scherpe hoek is een hoek waarvan de maat niet groter is dan 90 graden.

Een stompe hoek is een hoek groter dan 90 graden.

Een hoek wordt rechts genoemd als de maat 90 is.

In het geval dat het wordt gevormd door één ononderbroken rechte lijn en de graadmaat 180 is, wordt het ingezet genoemd.

Hoeken die een gemeenschappelijke zijde hebben, waarvan de tweede zijde doorloopt, worden aangrenzend genoemd. Ze kunnen scherp of bot zijn. Het snijpunt van de lijn vormt aangrenzende hoeken. Hun eigenschappen zijn als volgt:

De som van dergelijke hoeken zal gelijk zijn aan 180 graden (er is een stelling die dit bewijst). Daarom kan een ervan gemakkelijk worden berekend als de andere bekend is.
Uit het eerste punt volgt dat aangrenzende hoeken niet kunnen worden gevormd door twee stompe of twee scherpe hoeken.

Dankzij deze eigenschappen kan men altijd de graadmaat van een hoek berekenen, gegeven de waarde van een andere hoek, of in ieder geval de verhouding daartussen.

Verticale hoeken

Hoeken waarvan de zijden voortzettingen van elkaar zijn, worden verticaal genoemd. Elk van hun variëteiten kan als zo'n paar fungeren. Verticale hoeken zijn altijd gelijk aan elkaar.

Ze worden gevormd wanneer lijnen elkaar kruisen. Samen met hen zijn aangrenzende hoeken altijd aanwezig. Een hoek kan zowel aangrenzend zijn voor de ene als verticaal voor de andere.

Bij het overschrijden van een willekeurige lijn worden ook verschillende soorten hoeken overwogen. Zo'n lijn wordt een secans genoemd en vormt de overeenkomstige, eenzijdige en kruislingse hoeken. Ze zijn gelijk aan elkaar. Ze kunnen worden bekeken in het licht van de eigenschappen die verticale en aangrenzende hoeken hebben.

Het onderwerp hoeken lijkt dus vrij eenvoudig en begrijpelijk. Al hun eigenschappen zijn gemakkelijk te onthouden en te bewijzen. Het oplossen van problemen is niet moeilijk zolang de hoeken overeenkomen met een numerieke waarde. Al verder, wanneer de studie van zonde en cos begint, zul je veel complexe formules, hun conclusies en consequenties moeten onthouden. Tot die tijd kun je gewoon genieten van eenvoudige puzzels waarin je aangrenzende hoeken moet vinden.

Gelijk aan twee rechte hoeken .

Gegeven twee aangrenzende hoeken: AOB En WOS. Het is vereist om te bewijzen dat:

∠AOW+∠BOS=d+ D = 2d

Laten we herstellen vanaf het punt OVER naar een rechte lijn AC loodrecht OD. We hebben de hoek AOB in twee delen AOD en DOB verdeeld, zodat we kunnen schrijven:

AOB = ∠ AOD+∠ DOB

Laten we beide zijden van deze gelijkheid met dezelfde hoek optellen BOC, waarom de gelijkheid niet wordt geschonden:

∠ AOB + ∠ BOVAN= AOD + ∠ DOB + ∠ BOVAN

sinds het bedrag DOB + BOC is juiste hoek DOENVAN, dan

∠ AOB+ ∠ BOVAN= ∠ AOD + ∠ DOENVAN= D + D = 2 D,

QED

Gevolgen.

1. Som van hoeken (AOB,BOC, KABELJAUW, DOE) gelegen rond een gemeenschappelijk hoekpunt (O) aan één kant van de rechte lijn ( AE) is gelijk aan 2 D= 180 0 , omdat deze som de som van twee is aangrenzende hoeken, zoals: AOC + COE

2. Som van hoeken gelegen rond een gemeenschappelijke pieken (O) aan beide zijden van een rechte lijn is gelijk aan 4 d=360 0 ,

Inverse stelling.

Als som van twee hoeken, met een gemeenschappelijk hoekpunt en een gemeenschappelijke zijde en elkaar niet bedekken, is gelijk aan twee rechte hoeken (2d), dan zijn dergelijke hoeken - verwant, d.w.z. de andere twee kanten zijn rechte lijn.

Als we vanuit één punt (O) van een rechte (AB) loodlijnen daarop herstellen, op elk van zijn zijden, dan vormen deze loodlijnen één rechte lijn (CD). Vanaf elk punt buiten de lijn kun je naar deze lijn gaan loodrecht en slechts één.

Omdat som van hoeken MAÏSKOLF En BOD is gelijk aan 2d.

RechtdoorVAN delen waarvan OVAN En OD staan loodrecht op de lijn AB, heet een lijn loodrecht op AB.

als hetero VAND loodrecht op de lijn AB, en vice versa: AB loodrecht op VAND omdat onderdelen OA En OB dien ook loodrecht op VAND. Daarom, direct AB En VAND genaamd onderling loodrecht.

Dat twee rechte AB En VAND onderling loodrecht, schriftelijk uitgedrukt als AB^ VAND.

De twee hoeken heten verticaal als de zijkanten van de ene een voortzetting zijn van de zijkanten van de andere.

Dus, wanneer twee lijnen elkaar kruisen AB En VAND twee paar verticale hoeken worden gevormd: AOD En MAÏSKOLF; AOC En DOB .

Stelling.

Twee verticale hoek Gelijk .

Laat twee verticale hoeken worden gegeven: AOD En VANOB die. OB er is een vervolg OA, maar OVAN voortzetting OD.

Het is vereist om te bewijzen dat AOD = VANOB.

Volgens de eigenschap van aangrenzende hoeken kunnen we schrijven:

AOD + DOB= 2 D

DOB + BOC = 2d

Middelen: AOD + DOB = DOB + BOC.

Als je van beide delen hiervan aftrekt gelijkwaardigheid per hoek DOB, we krijgen:

AOD = BOC, dat moest worden bewezen.

Op een vergelijkbare manier zullen we bewijzen dat: AOC = DOB.

over het onderwerp: Aangrenzende en verticale hoeken, hun eigenschappen.

(3 lessen)

Als resultaat van het bestuderen van het onderwerp, heb je nodig:

IN STAAT ZIJN OM:

Begrippen: aangrenzende en verticale hoeken, loodrechte lijnen

Onderscheid maken tussen aangrenzende en verticale hoeken

Stellingen van aangrenzende en verticale hoeken

Problemen oplossen met eigenschappen van aangrenzende en verticale hoeken

Aangrenzende en verticale hoekeigenschappen

Construeer aangrenzende en verticale hoeken loodrecht op lijnen

LITERATUUR:

1. Geometrie. Groep 7. Zh Kaidasov, G. Dosmagambetova, V. Abdiev. Almaty "Mektep". 2012

2. Geometrie. Groep 7. KO Bukubaeva, A.T. Mirazov. AlmatyAtamura". 2012

3. Geometrie. Groep 7. Methodologische gids. KO Bukubaeva. AlmatyAtamura". 2012

4. Geometrie. Groep 7. Didactisch materiaal. A.N.Shynybekov. AlmatyAtamura". 2012

5. Geometrie. Groep 7. Verzameling van taken en oefeningen. KO Bukubaeva, A.T. Mirazova. AlmatyAtamura". 2012

Onthoud dat je volgens het algoritme moet werken!

Vergeet niet te slagen voor de test, maak aantekeningen in de kantlijn,

Laat alsjeblieft geen vragen onbeantwoord.

Wees objectief tijdens de peer review, het zal jou en de ander helpen

wie controleer je.

WENS JE SUCCES!

TAAK №1.

Lees de definitie en leer (2b):

Definitie. Hoeken waarvan de ene zijde gemeenschappelijk is en de andere twee zijden extra stralen worden aangrenzend genoemd.

2) Leer en noteer de stelling in je schrift: (2b)

De som van aangrenzende hoeken is 180.

Gegeven:

∠ ANM en∠ DOV - gegeven aangrenzende hoeken

OD - gemeenschappelijke kant

Bewijzen:

∠ AOD +∠ DOV = 180

Bewijs:

Gebaseerd op het axiomaIII 4:

∠ AOD +∠ DOV =∠ AOW.

∠ AOV - ingezet. Vervolgens,

∠ AOD +∠ DOV = 180

De stelling is bewezen.

3) Uit de stelling volgt: (2b)

1) Als twee hoeken gelijk zijn, dan zijn de aangrenzende hoeken gelijk;

2) als aangrenzende hoeken gelijk zijn, dan is de graadmaat van elk van hen 90 °.

Onthouden!

Een hoek gelijk aan 90° wordt een rechte hoek genoemd.

Een hoek kleiner dan 90° wordt een scherpe hoek genoemd.

Een hoek groter dan 90° en kleiner dan 180° wordt een stompe hoek genoemd.

Rechte hoek Scherpe hoek Stompe hoek

Aangezien de som van aangrenzende hoeken 180° is, dan is

1) een hoek grenzend aan een rechte hoek, rechts;

2) de hoek die grenst aan de scherpe hoek is stomp;

3) een hoek die grenst aan een stompe hoek is scherp.

4) Beschouw een voorbeeldoplossing hadachi:

een gegeven:∠ HkEn∠ kl- aangrenzend;∠ Hkmeer∠ klop 50°.

Vinden:∠ HkEn∠ kl.

Oplossing: laten we∠ kl= x, dan∠ Hk= x + 50°. Op eigenschap over de som van aangrenzende hoeken∠ kl + ∠ Hk= 180°.

x + x + 50° = 180°;

2x = 180° - 50°;

2x = 130°;

x = 65°.

∠ kl= 65°;∠ Hk= 65°+ 50° = 115°.

Antwoord: 115 ° en 65 °.

b) Laten we∠ kl= x, dan∠ Hk= 3x

x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.

Antwoord: 135° en 45°.

5) Werk met de definitie van aangrenzende hoeken: (2 b)

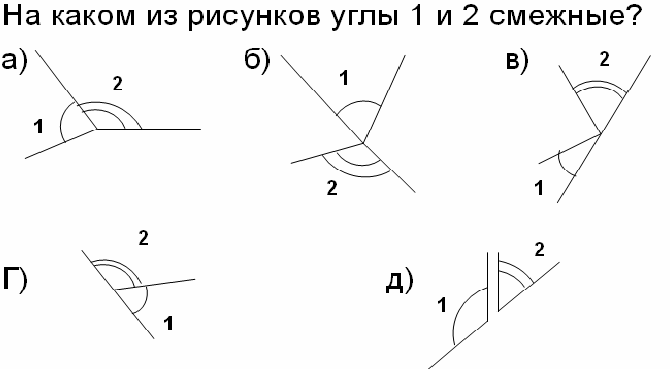
6) Zoek fouten in de definities: (2b)

Slaag voor test # 1

Taak nummer 2

1) Construeer 2 aangrenzende hoeken zodat hun gemeenschappelijke zijde door punt C gaat en de zijde van een van de hoeken samenvalt met de straal AB (2b)

2). Praktisch werk om de eigenschappen van aangrenzende hoeken te ontdekken: (5b)

Werkproces

1. Bouw een hoek opaangrenzende hoekmaar , alsmaar : scherp, recht, stomp.

2. Meet de hoeken.

3. Voer de meetgegevens in de tabel in.

4. Zoek de verhouding tussen de waarden van de hoekenmaar En.

5. Trek een conclusie over de eigenschap van aangrenzende hoeken.

Slaag voor test #2

Taak nummer 3

Onuitgevouwen tekenen∠ AOB en noem de stralen die de zijden van deze hoek zijn.

Trek straal O, die een voortzetting is van straal OA, en straal OD, die een voortzetting is van straal OB.

Schrijf in je notitieboekje: hoeken∠ AOB en∠ SOD worden verticaal genoemd. (3b)

Leren en schrijven in een notitieboekje: (4b)

Definitie: Hoeken waarvan de zijden van de ene complementaire stralen van de andere zijn, worden genoemdverticale hoeken.

< 1 en<2, <3 и <4 verticale hoeken

stralenVANEnOA , OCEnOEzijn paarsgewijs complementaire stralen.

Stelling: Verticale hoeken zijn gelijk.

Bewijs.

Verticale hoeken worden gevormd wanneer twee lijnen elkaar kruisen. Laat de lijnen a enBsnijden in punt O.∠ 1 en∠ 2 - verticale hoeken.

∠ AOC-ingezette middelen∠ AOC= 180°. maar∠ 1+ ∠ 2= ∠ AOC, d.w.z.

∠ 3+ ∠ 1= 180°, dus we hebben:

∠ 1= 180 - ∠ 3. (1)

Dat hebben we ook∠ DOV= 180°, vandaar∠ 2+ ∠ 3= 180° of∠ 2= 180°- ∠ 3. (2)

Aangezien in gelijkheden (1) en (2) de directe delen gelijk zijn, dan∠ 1= ∠ 2.

De stelling is bewezen.

vijf). Werk met de definitie van verticale hoeken: (2b)

6) Zoek een fout in de definitie: (2b).

Slaag voor test #3

Taak nummer 4

1) Praktisch werk om de eigenschappen van verticale hoeken te ontdekken: (5b)

Werkproces:

1. Construeer een hoek (verticale hoek)α , alsα :

scherp, recht, stomp.

2. Meet de hoeken.

3. Voer de meetgegevens in de tabel in

4. Zoek de relatie tussen de waarden van de hoeken α en β.

5. Maak een conclusie over de eigenschap van verticale hoeken.

2) Bewijs van eigenschappen van aangrenzende en verticale hoeken. (3b)

2) Overweeg een voorbeeldoplossinghel.

Een taak. Lijnen AB en CD snijden elkaar in punt O zodat∠ AOD = 35°. Zoek de hoeken AOC en BOC.

Oplossing:

1) Hoeken AOD en AOC zijn aangrenzend, dus∠ BOC= 180° - 35° = 145°.

2) Hoeken AOC en BOC zijn ook aangrenzend, dus∠ BOC= 180° - 145° = 35°.

Middelen,∠ BOC = ∠ AOD = 35°, en deze hoeken zijn verticaal. Vraag: Is het waar dat alle verticale hoeken gelijk zijn?

3) Problemen met voltooide tekeningen oplossen: (3b)

1. Zoek de hoeken AOB, AOD, COD.

3) Zoek de hoeken BOC, FOA.: (3b)

3. Zoek aangrenzende en verticale hoeken in de figuur. Laat de waarden van de twee hoeken die op de tekening zijn gemarkeerd bekend zijn, 28? en 90?. Is het mogelijk om de waarden van de resterende hoeken te vinden zonder metingen te doen (2b)

Slaag voor test # 4

Taak nummer 5

Test je kennis door in te vullenverificatie werk nr. 1

Taak nummer 6

1) Bewijs zelf de eigenschappen van verticale hoeken en noteer deze bewijzen in een schrift. (3b)

De leerlingen moeten zelfstandig, gebruikmakend van de eigenschappen van verticale en aangrenzende hoeken, onderbouwen dat als op het snijpunt van twee lijnen een van de gevormde hoeken een rechte is, dan zijn de andere hoeken ook goed.

2) Los twee problemen op om uit te kiezen:

1. Graadmaten van aangrenzende hoeken zijn gerelateerd als 7:2. Vind deze hoeken (2b)

2. Een van de hoeken gevormd op het snijpunt van twee lijnen is 11 keer kleiner dan de andere. Bepaal elk van de hoeken (3b)

3. Vind aangrenzende hoeken als hun verschil en hun som gerelateerd zijn als 2: 9. (3b)

Taak nummer 7

Goed gedaan! U kunt doorgaan met proefwerk nummer 2.

Verificatiewerk nr. 1.

Beslis over de keuze van een van de opties (10b)

Optie 1

<1 и <2,

<3 и <2,

G)<1 и <3. Какие это углы?

Verwant

e) Teken (met het oog) een hoek van 30° en< abc, naast het gegeven

f) Wat zijn de verticale hoeken?

Twee hoeken worden verticaal genoemd als de orni gelijk zijn.

g) Trek vanuit punt A twee lijnen loodrecht op de lijnmaar

Er kan slechts één rechte lijn worden getrokken.

Optie 2

1. De student, die de vragen van de leraar beantwoordde, gaf de juiste antwoorden. Controleer of ze juist zijn door in de derde kolom de woorden "JA", "NEE", "IK WEET NIET" aan te kruisen. Indien “NEE”, noteer daar het juiste antwoord of voeg het ontbrekende toe.

<1 и <4,

<2 и <4

D)<1 и < 3 смежные?

Nee. Ze zijn verticaal

E) Welke lijnen worden loodrecht genoemd?

Twee lijnen worden loodrecht genoemd als ze elkaar in een rechte hoek snijden.

G) Teken de verticale hoeken zodat hun zijden loodrechte lijnen zijn.