Hoe een geheel getal af te trekken van een onechte breuk. Breuken toevoegen

21.10.2019

Breuken zijn gewone getallen en kunnen ook worden opgeteld en afgetrokken. Maar vanwege het feit dat ze een noemer bevatten, meer complexe regels dan voor gehele getallen.

Laten we het eenvoudigste geval bekijken, wanneer er twee breuken zijn met dezelfde noemers. Dan:

Om breuken met dezelfde noemers op te tellen, moet je hun tellers optellen en de noemer ongewijzigd laten.

Om breuken met dezelfde noemers af te trekken, moet je de teller van de tweede aftrekken van de teller van de eerste breuk, en de noemer opnieuw ongewijzigd laten.

Binnen elke uitdrukking zijn de noemers van de breuken gelijk. Per definitie van het optellen en aftrekken van breuken krijgen we:

Zoals je kunt zien, is het niets ingewikkelds: we tellen gewoon de tellers op of trekken ze af, en dat is alles.

Maar zelfs bij zulke eenvoudige handelingen slagen mensen erin fouten te maken. Wat vaak wordt vergeten, is dat de noemer niet verandert. Als ze bijvoorbeeld worden opgeteld, beginnen ze ook op te tellen, en dit is fundamenteel verkeerd.

Van afkomen slechte gewoonte Het optellen van de noemers is vrij eenvoudig. Probeer hetzelfde bij het aftrekken. Als gevolg hiervan zal de noemer nul zijn en zal de breuk (plotseling!) zijn betekenis verliezen.

Onthoud daarom voor eens en altijd: bij het optellen en aftrekken verandert de noemer niet!

Veel mensen maken ook fouten bij het optellen van meerdere negatieve breuken. Er is verwarring met de tekens: waar moet een min worden geplaatst en waar moet een plus worden geplaatst.

Dit probleem is ook heel eenvoudig op te lossen. Het volstaat om te onthouden dat de min vóór het teken van een breuk altijd kan worden overgedragen naar de teller - en omgekeerd. En vergeet natuurlijk twee eenvoudige regels niet:

Plus door min geeft min;
Twee negatieven maken een bevestigend.

Laten we het allemaal opsplitsen specifieke voorbeelden:

Taak. Zoek de betekenis van de uitdrukking:

In het eerste geval is alles eenvoudig, maar in het tweede geval voegen we minnen toe aan de tellers van de breuken:

Wat te doen als de noemers verschillend zijn

Direct breuken optellen met verschillende noemers het is verboden. Althans, deze methode is mij onbekend. De oorspronkelijke breuken kunnen echter altijd worden herschreven, zodat de noemers hetzelfde worden.

Er zijn veel manieren om breuken om te zetten. Drie ervan worden besproken in de les 'Breuken herleiden tot een gemeenschappelijke noemer', dus we zullen er hier niet verder op ingaan. Laten we eens kijken naar enkele voorbeelden:

Taak. Zoek de betekenis van de uitdrukking:

In het eerste geval herleiden we de breuken tot een gemeenschappelijke noemer met behulp van de “criss-cross”-methode. In de tweede gaan we op zoek naar het NOC. Merk op dat 6 = 2 · 3; 9 = 3 · 3. De laatste factoren in deze uitbreidingen zijn gelijk, en de eerste zijn relatief priem. Daarom LCM(6, 9) = 2 3 3 = 18.

Wat te doen als een breuk een geheel getal heeft

Ik kan je een plezier doen: verschillende noemers in breuken zijn niet het grootste kwaad. Er treden veel meer fouten op als het hele onderdeel in de toegevoegde breuken wordt gemarkeerd.

Natuurlijk zijn er voor dergelijke breuken eigen optel- en aftrekkingsalgoritmen, maar deze zijn behoorlijk complex en vereisen een lange studie. Beter gebruiken eenvoudig diagram, onder aangegeven:

Converteer alle breuken die een geheel getal bevatten naar onechte breuken. We verkrijgen normale termen (zelfs met verschillende noemers), die worden berekend volgens de hierboven besproken regels;
Bereken feitelijk de som of het verschil van de resulterende breuken. Als resultaat zullen we praktisch het antwoord vinden;
Als dit alles is wat nodig was voor het probleem, voeren we de inverse transformatie uit, d.w.z. We verwijderen een onechte breuk door het hele deel te markeren.

De regels voor het overgaan naar onechte breuken en het markeren van het hele deel worden gedetailleerd beschreven in de les “Wat is een numerieke breuk”. Als u het zich niet herinnert, herhaal het dan. Voorbeelden:

Taak. Zoek de betekenis van de uitdrukking:

Alles is hier eenvoudig. De noemers binnen elke uitdrukking zijn gelijk, dus het enige wat overblijft is alle breuken om te zetten in onechte breuken en te tellen. We hebben:

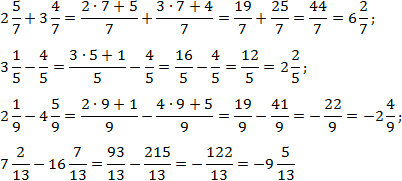
Om de berekeningen te vereenvoudigen, heb ik in de laatste voorbeelden enkele voor de hand liggende stappen overgeslagen.

Een kleine opmerking over de laatste twee voorbeelden, waarbij breuken met de gemarkeerde breuken worden afgetrokken hele deel. De min vóór de tweede breuk betekent dat de hele breuk wordt afgetrokken, en niet alleen het hele deel.

Herlees deze zin nog eens, kijk naar de voorbeelden - en denk erover na. Dit is waar beginners een groot aantal fouten maken. Ze geven er graag zulke taken aan testen. Je zult ze ook meerdere keren tegenkomen in de toetsen voor deze les, die binnenkort verschijnen.

Samenvatting: algemeen rekenschema

Tot slot zal ik een algemeen algoritme geven waarmee u de som of het verschil van twee of meer breuken kunt vinden:

Als een of meer breuken een geheel getal hebben, converteer deze breuken dan naar onechte breuken;
Breng alle breuken op een voor jou handige manier naar een gemeenschappelijke noemer (tenzij de schrijvers van de problemen dit natuurlijk hebben gedaan);
Voeg de resulterende getallen toe of trek ze af volgens de regels voor het optellen en aftrekken van breuken met gelijke noemers;
Verkort indien mogelijk het resultaat. Als de breuk onjuist is, selecteert u het hele deel.

Onthoud dat het beter is om het hele onderdeel helemaal aan het einde van de taak te markeren, onmiddellijk voordat u het antwoord opschrijft.

Gemengde breuken kunnen, net als eenvoudige breuken, worden afgetrokken. Wegnemen gemengde cijfers breuken, je moet een paar regels kennen voor het aftrekken. Laten we deze regels met voorbeelden bestuderen.

Gemengde breuken met gelijke noemers aftrekken.

Laten we een voorbeeld bekijken met de voorwaarde dat de gehele en fractionele delen die worden verkleind groter zijn dan respectievelijk de gehele en fractionele delen die worden afgetrokken. Onder dergelijke omstandigheden vindt aftrekking afzonderlijk plaats. We trekken het hele deel af van het hele deel, en fractioneel deel van fractioneel.

Laten we eens kijken naar een voorbeeld:

Trek gemengde breuken \(5\frac(3)(7)\) en \(1\frac(1)(7)\) af.

\(5\frac(3)(7)-1\frac(1)(7) = (5-1) + (\frac(3)(7)-\frac(1)(7)) = 4\ frac(2)(7)\)

De juistheid van de aftrekking wordt gecontroleerd door optelling. Laten we de aftrekking controleren:

\(4\frac(2)(7)+1\frac(1)(7) = (4 + 1) + (\frac(2)(7) + \frac(1)(7)) = 5\ frac(3)(7)\)

Laten we een voorbeeld bekijken met de voorwaarde dat het fractionele deel van de minuend kleiner is dan het overeenkomstige fractionele deel van de aftrekker. In dit geval lenen we er één uit het geheel in de minuend.

Laten we eens kijken naar een voorbeeld:

Trek gemengde breuken \(6\frac(1)(4)\) en \(3\frac(3)(4)\) af.

Het minuend \(6\frac(1)(4)\) heeft een kleiner fractioneel deel dan het fractionele deel van het aftrekkerstuk \(3\frac(3)(4)\). Dat wil zeggen: \(\frac(1)(4)< \frac{1}{3}\), поэтому сразу отнять мы не сможем. Займем у целой части у 6 единицу, а потом выполним вычитание. Единицу мы запишем как \(\frac{4}{4} = 1\)

\(\begin(uitlijnen)&6\frac(1)(4)-3\frac(3)(4) = (6 + \frac(1)(4))-3\frac(3)(4) = (5 + \kleur(rood) (1) + \frac(1)(4))-3\frac(3)(4) = (5 + \kleur(rood) (\frac(4)(4)) + \frac(1)(4))-3\frac(3)(4) = (5 + \frac(5)(4))-3\frac(3)(4) = \\\\ &= 5\frac(5)(4)-3\frac(3)(4) = 2\frac(2)(4) = 2\frac(1)(4)\\\\ \end(uitlijnen)\)

Volgend voorbeeld:

\(7\frac(8)(19)-3 = 4\frac(8)(19)\)

Een gemengde breuk aftrekken van een geheel getal.

Voorbeeld: \(3-1\frac(2)(5)\)

Minuend 3 heeft geen breukdeel, dus we kunnen niet onmiddellijk aftrekken. Laten we er één lenen van het hele deel van 3, en dan aftrekken. We zullen de eenheid schrijven als \(3 = 2 + 1 = 2 + \frac(5)(5) = 2\frac(5)(5)\)

\(3-1\frac(2)(5)= (2 + \kleur(rood) (1))-1\frac(2)(5) = (2 + \kleur(rood) (\frac(5 )(5)))-1\frac(2)(5) = 2\frac(5)(5)-1\frac(2)(5) = 1\frac(3)(5)\)

Gemengde breuken met verschillende noemers aftrekken.

Laten we een voorbeeld bekijken met de voorwaarde dat de breukdelen van het minuend en het aftrekkertje verschillende noemers hebben. Je moet het naar een gemeenschappelijke noemer brengen en vervolgens aftrekken.

Trek twee gemengde breuken af met verschillende noemers \(2\frac(2)(3)\) en \(1\frac(1)(4)\).

De gemeenschappelijke noemer zal het getal 12 zijn.

\(2\frac(2)(3)-1\frac(1)(4) = 2\frac(2 \times \kleur(rood) (4))(3 \times \kleur(rood) (4) )-1\frac(1 \times \kleur(rood) (3))(4 \times \kleur(rood) (3)) = 2\frac(8)(12)-1\frac(3)(12 ) = 1\frac(5)(12)\)

Vragen over het onderwerp:
Hoe gemengde breuken aftrekken? Hoe gemengde breuken op te lossen?
Antwoord: u moet beslissen tot welk type de expressie behoort en het oplossingsalgoritme toepassen op basis van het type expressie. Van het gehele deel trekken we het gehele getal af, van het breukdeel trekken we het breukdeel af.

Hoe trek je een breuk af van een geheel getal? Hoe trek je een breuk af van een geheel getal?
Antwoord: je moet een eenheid van een geheel getal nemen en deze eenheid als een breuk schrijven

\(4 = 3 + 1 = 3 + \frac(7)(7) = 3\frac(7)(7)\),

en trek dan het geheel af van het geheel, trek het fractionele deel af van het fractionele deel. Voorbeeld:

\(4-2\frac(3)(7) = (3 + \kleur(rood) (1))-2\frac(3)(7) = (3 + \kleur(rood) (\frac(7) )(7)))-2\frac(3)(7) = 3\frac(7)(7)-2\frac(3)(7) = 1\frac(4)(7)\)

Voorbeeld 1:
Trek een eigen breuk af van één: a) \(1-\frac(8)(33)\) b) \(1-\frac(6)(7)\)

Oplossing:
a) Laten we ons één voorstellen als een breuk met de noemer 33. We krijgen \(1 = \frac(33)(33)\)

\(1-\frac(8)(33) = \frac(33)(33)-\frac(8)(33) = \frac(25)(33)\)

b) Laten we ons één voorstellen als een breuk met de noemer 7. We krijgen \(1 = \frac(7)(7)\)

\(1-\frac(6)(7) = \frac(7)(7)-\frac(6)(7) = \frac(7-6)(7) = \frac(1)(7) \)

Voorbeeld #2:
Trek een gemengde breuk af van een geheel getal: a) \(21-10\frac(4)(5)\) b) \(2-1\frac(1)(3)\)

Oplossing:
a) Laten we 21 eenheden van het gehele getal lenen en het als volgt schrijven: \(21 = 20 + 1 = 20 + \frac(5)(5) = 20\frac(5)(5)\)

\(21-10\frac(4)(5) = (20 + 1)-10\frac(4)(5) = (20 + \frac(5)(5))-10\frac(4)( 5) = 20\frac(5)(5)-10\frac(4)(5) = 10\frac(1)(5)\\\\\)

b) Laten we er één nemen van het gehele getal 2 en deze als volgt schrijven: \(2 = 1 + 1 = 1 + \frac(3)(3) = 1\frac(3)(3)\)

\(2-1\frac(1)(3) = (1 + 1)-1\frac(1)(3) = (1 + \frac(3)(3))-1\frac(1)( 3) = 1\frac(3)(3)-1\frac(1)(3) = \frac(2)(3)\\\\\)

Voorbeeld #3:
Trek een geheel getal af van een gemengde breuk: a) \(15\frac(6)(17)-4\) b) \(23\frac(1)(2)-12\)

a) \(15\frac(6)(17)-4 = 11\frac(6)(17)\)

b) \(23\frac(1)(2)-12 = 11\frac(1)(2)\)

Voorbeeld #4:
Trek een eigen breuk af van een gemengde breuk: a) \(1\frac(4)(5)-\frac(4)(5)\)

\(1\frac(4)(5)-\frac(4)(5) = 1\\\\\)

Voorbeeld #5:
Bereken \(5\frac(5)(16)-3\frac(3)(8)\)

\(\begin(uitlijnen)&5\frac(5)(16)-3\frac(3)(8) = 5\frac(5)(16)-3\frac(3 \times \kleur(rood) ( 2))(8 \times \kleur(rood) (2)) = 5\frac(5)(16)-3\frac(6)(16) = (5 + \frac(5)(16))- 3\frac(6)(16) = (4 + \kleur(rood) (1) + \frac(5)(16))-3\frac(6)(16) = \\\\ &= (4 + \kleur(rood) (\frac(16)(16)) + \frac(5)(16))-3\frac(6)(16) = (4 + \kleur(rood) (\frac(21 )(16)))-3\frac(3)(8) = 4\frac(21)(16)-3\frac(6)(16) = 1\frac(15)(16)\\\\ \einde(uitlijnen)\)

In het artikel zullen we laten zien Hoe breuken op te lossen met behulp van eenvoudige, begrijpelijke voorbeelden. Laten we uitzoeken wat een breuk is en erover nadenken breuken oplossen!

Concept breuken wordt geïntroduceerd in wiskundecursussen vanaf de 6e klas van de middelbare school.

Breuken hebben de vorm: ±X/Y, waarbij Y de noemer is, het geeft aan in hoeveel delen het geheel is verdeeld, en X is de teller, het geeft aan hoeveel van zulke delen er zijn genomen. Laten we voor de duidelijkheid een voorbeeld nemen met een taart:

In het eerste geval werd de cake gelijk gesneden en werd de helft genomen, d.w.z. 1/2. In het tweede geval werd de cake in 7 delen gesneden, waarvan er 4 werden genomen, d.w.z. 4/7.

Als het deel van het delen van het ene getal door het andere geen geheel getal is, wordt het als een breuk geschreven.

De uitdrukking 4:2 = 2 geeft bijvoorbeeld een geheel getal, maar 4:7 is niet deelbaar door een geheel, dus deze uitdrukking wordt geschreven als een breuk 4/7.

Met andere woorden fractie is een uitdrukking die de deling van twee getallen of uitdrukkingen aangeeft, en die wordt geschreven met een gedeeltelijke schuine streep.

Als de teller kleiner is dan de noemer, is de breuk juist; andersom is het een onechte breuk. Een breuk kan een geheel getal bevatten.

Bijvoorbeeld 5 hele 3/4.

Deze invoer betekent dat om de hele 6 te krijgen, een deel van de vier ontbreekt.

Als je het wilt onthouden, Hoe breuken op te lossen voor het 6e leerjaar, dat moet je begrijpen breuken oplossen komt eigenlijk neer op het begrijpen van een paar eenvoudige dingen.

Een breuk is in wezen een uitdrukking van een breuk. Dat wil zeggen, een numerieke uitdrukking van welk onderdeel is gegeven waarde uit één geheel. De breuk 3/5 drukt bijvoorbeeld uit dat als we iets geheel in vijf delen verdelen en het aantal aandelen of delen van dit geheel drie is.
De breuk kan kleiner zijn dan 1, bijvoorbeeld 1/2 (of in wezen de helft), dan is het correct. Als de breuk groter is dan 1, bijvoorbeeld 3/2 (drie helften of anderhalf), dan is dit onjuist en om de oplossing te vereenvoudigen is het beter voor ons om het hele deel 3/2 = 1 geheel 1 te selecteren /2.
Breuken zijn dezelfde getallen als 1, 3, 10 en zelfs 100, alleen zijn de getallen geen hele getallen maar breuken. U kunt er dezelfde bewerkingen mee uitvoeren als met cijfers. Breuken tellen is niet moeilijker, en we zullen dit verder laten zien met specifieke voorbeelden.

Hoe breuken op te lossen. Voorbeelden.

Er is een grote verscheidenheid aan rekenkundige bewerkingen van toepassing op breuken.

Een breuk herleiden tot een gemeenschappelijke noemer

U moet bijvoorbeeld de breuken 3/4 en 4/5 vergelijken.

Om het probleem op te lossen, vinden we eerst de kleinste gemene deler, d.w.z. het kleinste getal dat deelbaar is door elk van de noemers van de breuken zonder een rest achter te laten

Kleinste gemene deler(4,5) = 20

Vervolgens wordt de noemer van beide breuken herleid tot de kleinste gemene deler

Antwoord: 15/20

Breuken optellen en aftrekken

Als het nodig is om de som van twee breuken te berekenen, worden ze eerst naar een gemeenschappelijke noemer gebracht, waarna de tellers worden opgeteld, terwijl de noemer ongewijzigd blijft. Het verschil tussen breuken wordt op dezelfde manier berekend, het enige verschil is dat de tellers worden afgetrokken.

U moet bijvoorbeeld de som van de breuken 1/2 en 1/3 vinden

Laten we nu het verschil vinden tussen de breuken 1/2 en 1/4

Breuken vermenigvuldigen en delen

Hier is het oplossen van breuken niet moeilijk, alles is hier vrij eenvoudig:

Vermenigvuldigen - tellers en noemers van breuken worden met elkaar vermenigvuldigd;
Delen - eerst krijgen we de breuk inverse van de tweede breuk, d.w.z. We wisselen de teller en de noemer om, waarna we de resulterende breuken vermenigvuldigen.

Bijvoorbeeld:

Dat is het zo'n beetje Hoe breuken op te lossen, Alle. Mocht u nog vragen hebben over breuken oplossen, als iets onduidelijk is, schrijf dan in de reacties en we zullen je zeker antwoorden.

Bent u docent, dan is het mogelijk om de presentatie te downloaden Lagere school(http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) zal van pas komen voor jou.

In de vijfde eeuw voor Christus formuleerde de oude Griekse filosoof Zeno van Elea zijn beroemde aporia's, waarvan de bekendste de 'Achilles en de schildpad'-aporia is. Hier is hoe het klinkt:

Laten we zeggen dat Achilles tien keer sneller rent dan de schildpad en duizend stappen achter hem staat. Gedurende de tijd die Achilles nodig heeft om deze afstand af te leggen, kruipt de schildpad honderd stappen in dezelfde richting. Wanneer Achilles honderd stappen loopt, kruipt de schildpad nog eens tien stappen, enzovoort. Het proces zal tot in het oneindige doorgaan, Achilles zal de schildpad nooit inhalen.

Deze redenering werd een logische schok voor alle volgende generaties. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Ze hielden allemaal op de een of andere manier rekening met Zeno's aporie. De schok was zo sterk dat " ... de discussies gaan tot op de dag van vandaag door; de wetenschappelijke gemeenschap is er nog niet in geslaagd tot een gemeenschappelijke mening te komen over de essentie van paradoxen ... wiskundige analyse, verzamelingenleer, nieuwe fysieke en filosofische benaderingen waren bij de studie van de kwestie betrokken. ; geen van hen werd een algemeen aanvaarde oplossing voor het probleem..."[Wikipedia, "Zeno's Aporia". Iedereen begrijpt dat ze voor de gek worden gehouden, maar niemand begrijpt waaruit het bedrog bestaat.

Vanuit wiskundig oogpunt heeft Zeno in zijn aporie duidelijk de overgang aangetoond van kwantiteit naar . Deze overgang impliceert toepassing in plaats van permanente. Voor zover ik het begrijp is het wiskundige apparaat voor het gebruik van variabele meeteenheden nog niet ontwikkeld, of nog niet toegepast op Zeno’s aporie. Het toepassen van onze gebruikelijke logica leidt ons in een val. Vanwege de traagheid van het denken passen we constante tijdseenheden toe op de wederkerige waarde. Vanuit fysiek oogpunt lijkt dit erop dat de tijd vertraagt totdat deze volledig stopt op het moment dat Achilles de schildpad inhaalt. Als de tijd stopt, kan Achilles de schildpad niet langer ontlopen.

Als we onze gebruikelijke logica omdraaien, valt alles op zijn plaats. Achilles loopt mee constante snelheid. Elk volgend segment van zijn pad is tien keer korter dan het vorige. Dienovereenkomstig is de tijd die wordt besteed aan het overwinnen ervan tien keer minder dan de vorige. Als we in deze situatie het concept van ‘oneindigheid’ toepassen, zou het juist zijn om te zeggen: ‘Achilles zal de schildpad oneindig snel inhalen.’

Hoe kun je deze logische valkuil vermijden? Blijf in constante tijdseenheden en schakel niet over naar wederkerige eenheden. In de taal van Zeno ziet het er als volgt uit:

In de tijd die Achilles nodig heeft om duizend stappen te lopen, kruipt de schildpad honderd stappen in dezelfde richting. Tijdens het volgende tijdsinterval dat gelijk is aan het eerste, zal Achilles nog eens duizend stappen rennen, en de schildpad zal honderd stappen kruipen. Nu is Achilles de schildpad achthonderd stappen voor.

Deze benadering beschrijft de werkelijkheid adequaat, zonder enige logische paradoxen. Maar dit is geen volledige oplossing voor het probleem. Einsteins uitspraak over de onweerstaanbaarheid van de lichtsnelheid lijkt sterk op Zeno’s aporia “Achilles and the Tortoise”. We moeten dit probleem nog steeds bestuderen, heroverwegen en oplossen. En de oplossing moet niet gezocht worden in oneindig grote aantallen, maar in meeteenheden.

Een andere interessante aporie van Zeno vertelt over een vliegende pijl:

Een vliegende pijl is bewegingloos, omdat hij op elk moment in rust is, en omdat hij op elk moment in rust is, is hij altijd in rust.

In deze aporie wordt de logische paradox heel eenvoudig overwonnen: het is voldoende om te verduidelijken dat op elk moment een vliegende pijl stilstaat op verschillende punten in de ruimte, wat in feite beweging is. Hier moet nog een ander punt worden opgemerkt. Vanaf één foto van een auto op de weg is het onmogelijk om het feit van zijn beweging of de afstand ernaartoe te bepalen. Om te bepalen of een auto rijdt, heb je twee foto's nodig die vanaf hetzelfde punt zijn genomen verschillende momenten tijd, maar de afstand kan er niet uit worden bepaald. Om de afstand tot een auto te bepalen, heb je twee foto's nodig die op een bepaald moment vanaf verschillende punten in de ruimte zijn genomen, maar daaruit kun je het feit van beweging niet bepalen (je hebt natuurlijk nog steeds aanvullende gegevens nodig voor berekeningen, trigonometrie zal je helpen ). Waar ik op wil wijzen Speciale aandacht, is dat twee punten in de tijd en twee punten in de ruimte verschillende dingen zijn die niet verward mogen worden, omdat ze verschillende onderzoeksmogelijkheden bieden.

Woensdag 4 juli 2018

De verschillen tussen set en multiset worden heel goed beschreven op Wikipedia. Laten we eens kijken.

Zoals je kunt zien, ‘kunnen er geen twee identieke elementen in een set zitten’, maar als er identieke elementen in een set zitten, wordt zo’n set een ‘multiset’ genoemd. Redelijke wezens zullen zo’n absurde logica nooit begrijpen. Dit is het niveau van pratende papegaaien en getrainde apen, die geen verstand hebben van het woord ‘volledig’. Wiskundigen fungeren als gewone trainers en prediken ons hun absurde ideeën.

Er waren eens de ingenieurs die de brug bouwden in een boot onder de brug terwijl ze de brug testten. Als de brug instortte, stierf de middelmatige ingenieur onder het puin van zijn creatie. Als de brug de belasting kon weerstaan, bouwde de getalenteerde ingenieur andere bruggen.

Hoe wiskundigen zich ook verschuilen achter de uitdrukking ‘let op mij, ik ben in huis’, of beter gezegd: ‘wiskunde bestudeert abstracte concepten’, er is één navelstreng die ze onlosmakelijk met de werkelijkheid verbindt. Deze navelstreng is geld. Laten we de wiskundige verzamelingenleer toepassen op wiskundigen zelf.

We hebben heel goed wiskunde gestudeerd en nu zitten we aan de kassa salarissen uit te delen. Dus een wiskundige komt naar ons toe voor zijn geld. We tellen het hele bedrag voor hem af en leggen het in verschillende stapels op onze tafel, waarin we bankbiljetten van dezelfde waarde leggen. Vervolgens nemen we van elke stapel één rekening en geven de wiskundige zijn ‘wiskundige set salaris’. Laten we de wiskundige uitleggen dat hij de resterende rekeningen alleen zal ontvangen als hij bewijst dat een verzameling zonder identieke elementen niet gelijk is aan een verzameling met identieke elementen. Dit is waar het plezier begint.

Allereerst zal de logica van de afgevaardigden werken: “Dit kan op anderen worden toegepast, maar niet op mij!” Dan zullen ze ons beginnen gerust te stellen dat biljetten van dezelfde denominatie verschillende biljetnummers hebben, wat betekent dat ze niet als dezelfde elementen kunnen worden beschouwd. Oké, laten we de salarissen in munten tellen - er staan geen cijfers op de munten. Hier zal de wiskundige zich verwoed de natuurkunde gaan herinneren: er zijn verschillende munten verschillende hoeveelheden vuil, kristalstructuur en atomaire opstelling van elke munt is uniek...

En nu heb ik de meest interessante vraag: waar ligt de grens waarboven de elementen van een multiset veranderen in elementen van een set en omgekeerd? Zo'n lijn bestaat niet - alles wordt beslist door sjamanen, de wetenschap is hier niet eens in de buurt van leugens.

Kijk hier. Wij selecteren voetbalstadions met hetzelfde veldoppervlak. De oppervlakten van de velden zijn hetzelfde - wat betekent dat we een multiset hebben. Maar als we naar de namen van dezelfde stadions kijken, krijgen we er veel, omdat de namen verschillend zijn. Zoals je kunt zien, is dezelfde set elementen zowel een set als een multiset. Welke is correct? En hier haalt de wiskundige-sjamaan-scherpte een troefaas uit zijn mouw en begint ons te vertellen over een set of een multiset. Hoe dan ook, hij zal ons overtuigen van zijn gelijk.

Om te begrijpen hoe moderne sjamanen met de verzamelingenleer omgaan en deze aan de werkelijkheid koppelen, volstaat het om één vraag te beantwoorden: hoe verschillen de elementen van de ene verzameling van de elementen van een andere verzameling? Ik zal het je laten zien, zonder enig 'denkbaar als niet één geheel' of 'niet denkbaar als één geheel'.

Zondag 18 maart 2018

De som van de cijfers van een getal is een dans van sjamanen met een tamboerijn, wat niets met wiskunde te maken heeft. Ja, in wiskundelessen wordt ons geleerd de som van de cijfers van een getal te vinden en die te gebruiken, maar daarom zijn ze sjamanen, om hun nakomelingen hun vaardigheden en wijsheid te leren, anders sterven sjamanen eenvoudigweg uit.

Heb je bewijs nodig? Open Wikipedia en probeer de pagina 'Som van cijfers van een getal' te vinden. Ze bestaat niet. Er bestaat geen formule in de wiskunde die gebruikt kan worden om de som van de cijfers van welk getal dan ook te vinden. Cijfers zijn dat tenslotte grafische symbolen, met behulp waarvan we getallen schrijven en in de taal van de wiskunde klinkt de taak als volgt: "Vind de som van grafische symbolen die een willekeurig getal vertegenwoordigen." Wiskundigen kunnen dit probleem niet oplossen, maar sjamanen kunnen het gemakkelijk doen.

Laten we eens kijken wat en hoe we moeten doen om de som van de cijfers van een bepaald getal te vinden. En dus nemen we het getal 12345. Wat moet er gedaan worden om de som van de cijfers van dit getal te vinden? Laten we alle stappen in volgorde bekijken.

1. Schrijf het nummer op een vel papier. Wat hebben we gedaan? We hebben het getal omgezet in een grafisch getalsymbool. Dit is geen wiskundige bewerking.

2. Knip één resulterende afbeelding in verschillende afbeeldingen met individuele nummers. Het knippen van een afbeelding is geen wiskundige bewerking.

3. Converteer individuele grafische symbolen naar cijfers. Dit is geen wiskundige bewerking.

4. Voeg de resulterende getallen toe. Dit is nu wiskunde.

De som van de cijfers van het getal 12345 is 15. Dit zijn de ‘knip- en naaicursussen’ van sjamanen die wiskundigen gebruiken. Maar dat is niet alles.

Wiskundig gezien maakt het niet uit in welk getalsysteem we een getal schrijven. Dus, binnen verschillende systemen Bij calculus zal de som van de cijfers van hetzelfde getal verschillend zijn. In de wiskunde wordt het getallenstelsel aangegeven als een subscript rechts van het getal. Met het grote nummer 12345 wil ik mijn hoofd niet voor de gek houden, laten we het nummer 26 uit het artikel eens bekijken. Laten we dit getal schrijven in binaire, octale, decimale en hexadecimale getalsystemen. We zullen niet elke stap onder een microscoop bekijken; dat hebben we al gedaan. Laten we naar het resultaat kijken.

Zoals u kunt zien, is in verschillende getalsystemen de som van de cijfers van hetzelfde getal verschillend. Dit resultaat heeft niets met wiskunde te maken. Het is hetzelfde alsof je de oppervlakte van een rechthoek in meters en centimeters zou bepalen, je zou totaal andere resultaten krijgen.

Nul ziet er in alle getalstelsels hetzelfde uit en heeft geen som van cijfers. Dit is een ander argument vóór het feit dat. Vraag voor wiskundigen: hoe wordt in de wiskunde iets dat geen getal is, aangeduid? Wat, voor wiskundigen bestaat er niets behalve getallen? Voor sjamanen kan ik dit toestaan, maar niet voor wetenschappers. De werkelijkheid gaat niet alleen over cijfers.

Het verkregen resultaat moet worden beschouwd als bewijs dat getalsystemen meeteenheden voor getallen zijn. We kunnen immers geen getallen met verschillende meeteenheden vergelijken. Als dezelfde acties met verschillende meeteenheden van dezelfde hoeveelheid na vergelijking tot verschillende resultaten leiden, heeft dit niets met wiskunde te maken.

Wat is echte wiskunde? Dit is wanneer het resultaat van een wiskundige bewerking niet afhankelijk is van de grootte van het getal, de gebruikte meeteenheid en van wie deze actie uitvoert.

Teken op de deur Hij doet de deur open en zegt:

Oh! Is dit niet het damestoilet?
- Jonge vrouw! Dit is een laboratorium voor de studie van de onaantastbare heiligheid van zielen tijdens hun hemelvaart! Halo bovenaan en pijl omhoog. Welk ander toilet?

Vrouwtje... De halo bovenaan en de pijl naar beneden zijn mannelijk.

Als zo’n designkunstwerk meerdere keren per dag voor je ogen flitst,

Dan is het niet gek dat je ineens een vreemd icoontje in je auto aantreft:

Persoonlijk doe ik mijn best om bij een poepend persoon min vier graden te zien (één foto) (een compositie van meerdere foto's: een minteken, het getal vier, een aanduiding van graden). En ik denk niet dat dit meisje een dwaas is die geen natuurkunde kent. Ze heeft gewoon een sterk stereotype over het waarnemen van grafische beelden. En wiskundigen leren ons dit voortdurend. Hier is een voorbeeld.

1A is niet “min vier graden” of “één a”. Dit is "poepende man" of het getal "zesentwintig" in hexadecimale notatie. De mensen die voortdurend in dit getallensysteem werken, zien een cijfer en een letter automatisch als één grafisch symbool.

Acties met breuken. In dit artikel zullen we voorbeelden bekijken, alles in detail met uitleg. We zullen het overwegen gewone breuken. We zullen later naar decimalen kijken. Ik raad aan om het geheel te bekijken en achtereenvolgens te bestuderen.

1. Som van breuken, verschil van breuken.

Regel: bij het optellen van breuken met gelijke noemers is het resultaat een breuk - waarvan de noemer hetzelfde blijft en de teller gelijk is aan de som van de tellers van de breuken.
Regel: bij het berekenen van het verschil tussen breuken met dezelfde noemers krijgen we een breuk - de noemer blijft hetzelfde en de teller van de tweede wordt afgetrokken van de teller van de eerste breuk.

Formele notatie voor de som en het verschil van breuken met gelijke noemers:

Voorbeelden (1):

Het is duidelijk dat wanneer gewone breuken worden gegeven, alles eenvoudig is, maar wat als ze gemengd zijn? Niets ingewikkelds...

Optie 1– je kunt ze omzetten in gewone en ze vervolgens berekenen.

Optie 2– je kunt afzonderlijk “werken” met de gehele en gebroken delen.

Voorbeelden (2):

Meer:

Wat als het verschil tussen twee gemengde breuken wordt gegeven en de teller van de eerste breuk kleiner is dan de teller van de tweede? Je kunt ook op twee manieren handelen.

Voorbeelden (3):

*Omgerekend naar gewone breuken, het verschil berekend, de resulterende onechte breuk omgerekend naar een gemengde breuk.

*We hebben het opgesplitst in gehele en gebroken delen, kregen een drie, presenteerden vervolgens 3 als de som van 2 en 1, waarbij één werd weergegeven als 11/11, vonden vervolgens het verschil tussen 11/11 en 7/11 en berekenden het resultaat . De betekenis van de bovenstaande transformaties is om een eenheid te nemen (selecteren) en deze in de vorm van een breuk te presenteren met de noemer die we nodig hebben, waarna we een andere van deze breuk kunnen aftrekken.

Een ander voorbeeld:

Conclusie: er is een universele benadering - om de som (verschil) van gemengde breuken met gelijke noemers te berekenen, kunnen ze altijd worden omgezet in oneigenlijke breuken en vervolgens worden uitgevoerd Vereiste actie. Als het resultaat hierna een onechte breuk is, converteren we deze naar een gemengde breuk.

Hierboven hebben we gekeken naar voorbeelden met breuken die gelijke noemers hebben. Wat als de noemers verschillend zijn? In dit geval worden de breuken teruggebracht tot dezelfde noemer en wordt de opgegeven actie uitgevoerd. Om een breuk te veranderen (transformeren), wordt de basiseigenschap van de breuk gebruikt.

Laten we naar eenvoudige voorbeelden kijken:

In deze voorbeelden zien we meteen hoe een van de breuken kan worden getransformeerd om gelijke noemers te krijgen.

Als we manieren aanwijzen om breuken tot dezelfde noemer te herleiden, dan noemen we deze METHODE EEN.

Dat wil zeggen dat je bij het 'evalueren' van een breuk onmiddellijk moet uitzoeken of deze aanpak zal werken - we controleren of de grotere noemer deelbaar is door de kleinere. En als het deelbaar is, voeren we de transformatie uit: we vermenigvuldigen de teller en de noemer zodat de noemers van beide breuken gelijk worden.

Kijk nu eens naar deze voorbeelden:

Deze aanpak is niet op hen van toepassing. Er zijn ook manieren om breuken terug te brengen tot een gemeenschappelijke noemer; laten we ze eens bekijken.

Methode TWEE.

We vermenigvuldigen de teller en de noemer van de eerste breuk met de noemer van de tweede, en de teller en de noemer van de tweede breuk met de noemer van de eerste:

*In feite reduceren we breuken tot ze ontstaan als de noemers gelijk worden. Vervolgens gebruiken we de regel voor het optellen van breuken met gelijke noemers.

Voorbeeld:

*Deze methode is universeel te noemen en werkt altijd. Het enige nadeel is dat je na de berekeningen mogelijk een fractie overhoudt die verder moet worden verlaagd.

Laten we eens kijken naar een voorbeeld:

Het is duidelijk dat de teller en de noemer deelbaar zijn door 5:

Methode DRIE.

U moet het kleinste gemene veelvoud (LCM) van de noemers vinden. Dit zal de gemeenschappelijke noemer zijn. Wat voor nummer is dit? Dit is het minste natuurlijk nummer, die deelbaar is door elk van de getallen.

Kijk, hier zijn twee getallen: 3 en 4, er zijn veel getallen die door hen deelbaar zijn - dit zijn 12, 24, 36, ... De kleinste daarvan is 12. Of 6 en 15, 30, 60, 90 zijn deelbaar door hen.... Het kleinste getal is 30. De vraag is: hoe bepaal je dit kleinste gemene veelvoud?

Er is een duidelijk algoritme, maar vaak kan dit meteen zonder berekeningen. Volgens de bovenstaande voorbeelden (3 en 4, 6 en 15) is er bijvoorbeeld geen algoritme nodig, we hebben grote getallen (4 en 15) genomen, deze verdubbeld en gezien dat ze deelbaar zijn door het tweede getal, maar paren getallen kunnen andere zijn, bijvoorbeeld 51 en 119.

Algoritme. Om het kleinste gemene veelvoud van meerdere getallen te bepalen, moet je:

- Ontleed elk getal in EENVOUDIGE factoren

– noteer de ontbinding van de GROTERE ervan

- vermenigvuldig het met de ONTBREKENDE factoren van andere getallen

Laten we naar voorbeelden kijken:

50 en 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

in ontbinding meeréén vijf ontbreekt

=> LCM(50,60) = 2∙2∙3∙5∙5 = 300

48 en 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

bij de uitbreiding van een groter nummer ontbreken twee en drie

=> LCM(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Kleinste gemene veelvoud van twee priemgetallen gelijk aan hun product

Vraag! Waarom is het nuttig om het kleinste gemene veelvoud te vinden, aangezien je de tweede methode kunt gebruiken en eenvoudigweg de resulterende breuk kunt verkleinen? Ja, dat kan, maar het is niet altijd handig. Kijk naar de noemer van de getallen 48 en 72 als je ze simpelweg vermenigvuldigt met 48∙72 = 3456. Je zult het ermee eens zijn dat het prettiger is om met kleinere getallen te werken.

Laten we naar voorbeelden kijken:

*51 = 3∙17 119 = 7∙17

bij de uitbreiding van een groter aantal ontbreekt een triple

=> NOC(51,119) = 3∙7∙17

Laten we nu de eerste methode gebruiken:

*Kijk naar het verschil in de berekeningen, in het eerste geval zijn er een minimum, maar in het tweede geval moet je apart op een vel papier werken, en zelfs het deel dat je hebt ontvangen moet worden verminderd. Het vinden van de LOC vereenvoudigt het werk aanzienlijk.

Meer voorbeelden:

*In het tweede voorbeeld is het al duidelijk dat het kleinste getal dat deelbaar is door 40 en 60 120 is.

RESULTAAT! ALGEMEEN COMPUTERALGORITME!
— we reduceren breuken tot gewone breuken als er een geheel getal is.
- we brengen breuken naar een gemeenschappelijke noemer (eerst kijken we of de ene noemer deelbaar is door een andere; als deze deelbaar is, dan vermenigvuldigen we de teller en de noemer van deze andere breuk; als deze niet deelbaar is, handelen we met behulp van de andere methoden hierboven aangegeven).
- Nadat we breuken met gelijke noemers hebben ontvangen, voeren we bewerkingen uit (optellen, aftrekken).
- indien nodig verminderen we het resultaat.
- selecteer indien nodig het hele onderdeel.

2. Product van breuken.

De regel is eenvoudig. Bij het vermenigvuldigen van breuken worden hun tellers en noemers vermenigvuldigd:

Voorbeelden: